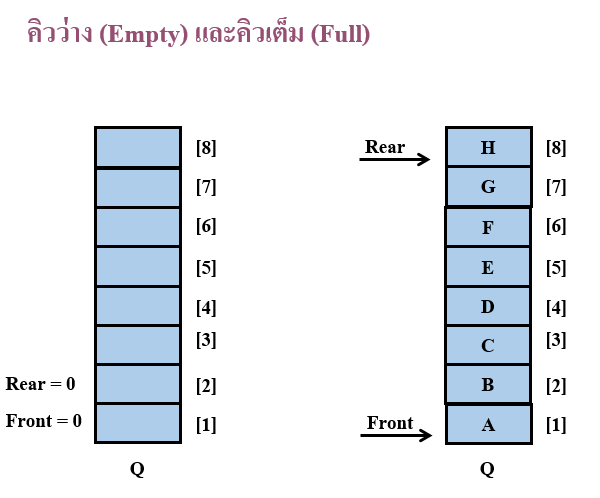
bubble sort
- เริ่มจากการนำค่าแรก มาเปรียบเทียบกับค่าถัดไป ซึ่งก็คือค่าที่สองในแถวลำดับ ถ้าไม่ตรงตามจุดประสงค์จะทำการสลับค่าทั้งสอง จากนั้นขยับมาเปรียบเทียบ ระหว่างค่า ที่ 2 และที่ 3 ทำเช่นนี้ไปเรื่อยๆ จนกว่าจะถึงค่าสุดท้าย ก็จะได้ค่าที่เรียงแล้วค่าแรกอยู่ ณ ตำแหน่งสุดท้ายของ แถวลำดับ
- ดำเนินการเช่นเดียวกับข้อ 1. โดยเริ่มต้น จากการเปรียบเทียบ ค่าที่ 2 กับ ค่าที่ 3 และเปรียบเทียบ ทีละคู่ไปเรื่อย ๆ จนถึงค่า รองสุดท้าย ก็จะได้ค่าที่เรียงแล้ว ค่าที่ 2 อยู่ ณ ตำแหน่งรองสุดท้าย ของแถวลำดับ
- ดำเนินการเช่นเดียวกับข้อ 1. จนครบทุกค่า ก็จะได้แถวลำดับที่เรียง
int num[5]={5,4,3,2,1};int i,j,temp;for(i=0;i<4;i++){for(j=0;j<4;j++){if(num[j]>num[j+1]){temp=num[j];num[j]=num[j+1];num[j+1]=temp;}}}
insertion sort
- นำข้อมูล 2 ตัวแรกเปรียบเทียบแล้วเรียงลำดับกันก่อน
- นำข้อมูลตัวถัดไปเปรียบเทียบตั้งแต่ตัวแรกของทางฝั่งซ้ายแล้วนำไปแทรกในตำแหน่งที่เหมาะสมที่สุด ทำขั้นตอนนี้ไปเรื่อยจนกว่าจะหมดข้อมูลทางด้านขวา ก็จะได้ผลลัพธ์ในการเรียงลำดับ
void insertionSort(int arr[]) {
for(int i=0; i< arr.length; i++) {
int value = arr[i];
int j = i-1;
while( j>=0 and arr[j]>value ) {
arr[j + 1] = arr[j]
j--;
}
arr[j+1] = value ;
}
}
Selection Sort
- เริ่มจากการนำ ค่าแรก มาเทียบกับค่าที่สองของแถวลำดับ ถ้าค่าแรก ค่าแรกมากกว่าค่าที่สอง จะทำการสลับค่าทั้งสองทำเช่นนี้ไปเรื่อยๆ โดยการนำค่าแรก มาเทียบกับค่าที่สาม , ค่าที่สี่, . . . , ค่าสุดท้าย เพื่อย้ายค่าที่มีค่าน้อยที่สุดมาอยู่ ณ ตำแหน่งแรก ของแถวลำดับ และเมื่อสิ้นสุดก็ถือว่าค่าแรก เป็นค่าที่เรียงแล้วในแถวลำดับ
- ดำเนินการเช่นเดียวกับข้อ 1. โดยการนำค่าที่สอง มาเทียบกับค่าถัดไปจนครบทุกค่าของแถวลำดับ เพื่อย้ายข้อมูลที่มีค่าน้อยที่สุดเป็นลำดับสอง มาอยู่ ณ ตำแหน่งที่สองของแถวลำดับ
- ดำเนินการเช่นเดียวกับข้อ 1. กับค่าที่สาม, ค่าที่สี่ ไปเรื่อยๆ จนถึง ค่ารองสุดท้าย ของแถวลำดับ ซึ่งในที่สุดจะได้ชุดข้อมูลในแถวลำดับที่เรียงกันตามความต้องการ
SelectionSort(Var : A[Max])
For (I := 1 to Max-1)
For (J := I+1 to Max) Do
If(A[I] > A[J]) Then Swape(A[I],A[J]);
Merge sort
เริ่มด้วยการแบ่งข้อมูลออกเป็นส่วนที่เล็กที่สุด แล้วเริ่มผสานข้อมูลก้อนเล็ก ๆ เข้าด้วยกันกลายเป็นข้อมูลก้อนที่ใหญ่ขึ้นในที่สุดข้อมูลทุกชิ้นจะเรียงลำดับอย่างสมบูรณ์
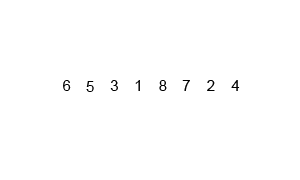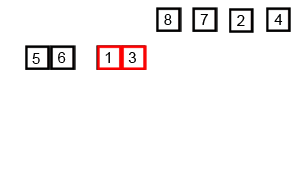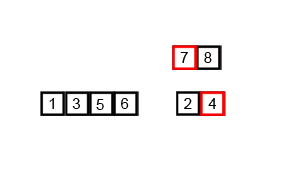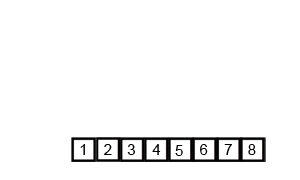
void merge_sort(int low, int high, int* p){int pivot;static int i(1);if (high>low){pivot = low + ((high - low)/2);merge_sort(low, pivot, p);merge_sort(pivot+1, high, p);merge(low, pivot, high, p);}}void merge(int l, int pi, int h,int* arr){int start = l;int mid = pi+1;while((start<=pi)&&(mid <=h)){if (arr[start] > arr[mid]){int temp = arr[mid];arr[mid] = arr[start];arr[start] = temp;mid++;}elsestart++;}}
Quick Sort
quicksort เป็น divide & conquer คือ
ถ้ามีข้อมูลชุดนึงที่เรียงแล้ว(น้อย->มาก) นำตัวตรงกลางๆ ออกมา ตัวนั้นต้องมีสมบัติดังนี้คือ ต้องมากกว่าข้อมูลทางซ้ายทั้งหมดและน้อยกว่าข้อมูลทางขวาทั้งหมด
เพราะฉะนั้นถ้าทำให้เราสามารถหยิบทุกตัวในข้อมูลแล้วมีคุณสมบัติตามนี้หมด (ยกเว้นกรณีหยิบซ้ายสุดขวาสุดนะ) ก็จะได้ว่าข้อมูลถูกเรียงแล้ว
เพราะฉะนั้นเวลาเขียน quicksort ก็จะมี function นึงที่เลือกข้อมูลมาตัวนึงมาจัดให้ด้านซ้ายน้อยกว่ามันหมด และทางขวามากกว่ามันหมด
แล้วทำซ้ำแบบเดิมด้วยการใช้ function เดิมกับข้อมูลด้านซ้าย และด้านขวา
int quickSort( int a[], int l, int r)
{
int j;
if( l < r )
{
// divide and conquer
j = partition( a, l, r);
quickSort( a, l, j-1);
quickSort( a, j+1, r);
}
return(0);
}
int partition( int a[], int l, int r) {
int pivot, i, j, t;
pivot = a[l];
i = l; j = r+1;
while( 1)
{
do ++i; while( a[ i ] <= pivot && i <= r );
do --j; while( a[j] > pivot );
if( i >= j ) break;
t = a[ i ]; a[ i ] = a[j]; a[j] = t;
}
t = a[l]; a[l] = a[j]; a[j] = t;
return j;
}